Fast Math Tricks & Shortcuts | Champions'Square

Simplification Techniques and Tricks - PDF

Simplification is one of the most important parts of Quantitative Aptitude section of any competitive exam. Today I am sharing all the techniques to solve Simplification questions quickly.

Rules of Simplification

V → Vinculum

B → Remove Brackets - in the order ( ) , { }, [ ] 

O → Of

D → Division

M → Multiplication

A → Addition

S → Subtraction

Important Parts of Simplification

• Number System
• HCF & LCM
• Square & Cube
• Fractions & Decimals
• Surds & Indices

Number System

• Classification
• Divisibility Test
• Division& Remainder Rules
• Sum Rules

 Classification 

Types	Description
Natural Numbers:	all counting numbers ( 1,2,3,4,5....∞)
Whole Numbers:	natural number + zero( 0,1,2,3,4,5...∞)
Integers:	All whole numbers including Negative number + Positive number(∞......-4,-3,-2,-1,0,1,2,3,4,5....∞)
Even & Odd Numbers :	All whole number divisible by 2 is Even (0,2,4,6,8,10,12.....∞) and which does not divide by 2 are Odd (1,3,5,7,9,11,13,15,17,19....∞)
Prime Numbers:	It can be positive or negative except 1, if the number is not divisible by any number except the number itself.(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61....∞)
Composite Numbers:	Natural numbers which are not prime
Co-Prime:	Two natural number a and b are said to be co-prime if their HCF is 1.

Divisibility

Numbers	IF A Number	Examples
Divisible by 2	End with 0,2,4,6,8 are divisible by 2	254,326,3546,4718 all are divisible by 2
Divisible by 3	Sum of its digits  is divisible by 3	375,4251,78123 all are divisible by 3.  [549=5+4+9][5+4+9=18]18 is divisible by 3  hence 549 is divisible by 3.
Divisible by 4	Last two digit divisible by 4	5648 here last 2 digits are 48 which is divisible by 4 hence 5648 is also divisible by 4.
Divisible by 5	Ends with 0 or 5	225 or 330 here last digit digit is 0 or 5 that mean both the numbers are divisible by 5.
Divisible by 6	Divides by Both 2 & 3	4536 here last digit is 6 so it divisible by 2 & sum of its digit (like 4+5+3+6=18) is 18 which is divisible by 3.Hence 4536 is divisible by 6.
Divisible by 8	Last 3 digit divide by 8	746848 here last 3 digit 848 is divisible by 8 hence 746848 is also divisible by 8.
Divisible by 10	End with 0	220,450,1450,8450 all numbers has a last digit zero it means all are divisible by 10.
Divisible by 11	[Sum of its digit in  odd places-Sum of its digits in even places]= 0 or multiple of 11	Consider the number 39798847  (Sum of its digits at odd places)-(Sum of its digits at even places)(7+8+9+9)-(4+8+7+3) (23-12) 23-12=11, which is divisible by 11. So 39798847 is divisible by 11.

Division & Remainder Rules

Suppose we divide 45 by 6

hence ,represent it as:

dividend = ( divisor✘quotient ) + remainder

or

divisior= [(dividend)-(remainder] / quotient

could be write it as 

x = kq + r where (x = dividend,k = divisor,q = quotient,r = remainder)

Example:

On dividing a certain number by 342, we get 47 as remainder. If the same number is divided by 18, what will be the remainder ?

Number = 342k + 47

( 18 ✘19k ) + ( 18 ✘2 ) + 11

18 ✘( 19k + 2 ) +11.

Remainder = 11

Sum Rules

(1+2+3+.........+n) = ¹/₂ n(n+1)

(1²+2²+3²+.........+n²) = ¹/₆ n (n+1) (2n+1)

(1³+2³+3³+.........+n³) = ¹/4 n² (n+1)²

Arithmetic Progression (A.P.)

a, a + d, a + 2d, a + 3d, ....are said to be in A.P. in which first term = a and common difference = d.

Let the nth term be t_n and last term = l, then

a) nth term = a + ( n - 1 ) d
b) Sum of n terms = ⁿ/₂ [2a + (n-1)d]
c) Sum of n terms = ⁿ/₂ (a+l) where l is the last term

• 
  

H.C.F. & L.C.M.

• Factorization & Division Method
• HCF & LCM of Fractions & Decimal Fractions

Methods

On Basis	H.C.F. or G.C.M	L.C.M.
Factorization Method	Write each number as the product of the prime factors. The product of least powers of common prime factors gives H.C.F. Example: Find the H.C.F. of 108, 288 and 360. 108 = 22✘33, 288 = 25✘32 and 360 = 23✘5✘32 H.C.F. = 22✘32=36	Write each number into a product of prime factors. Then, L.C.M is the product of highest powers of all the factors. Examples: Find the L.C.M. of 72, 108 and 2100. 72=23✘32,108=33✘22, 2100=22✘52✘3✘7. L.C.M.=23✘33✘52✘7=37800
Division Method	Let we have two numbers.Pick the smaller one and divide it by the larger one. After that divide the divisor with the remainder. This process of dividing the preceding number by the remainder will be repeated until we got the zero as remainder.The last divisor is the required H.C.F. Example: 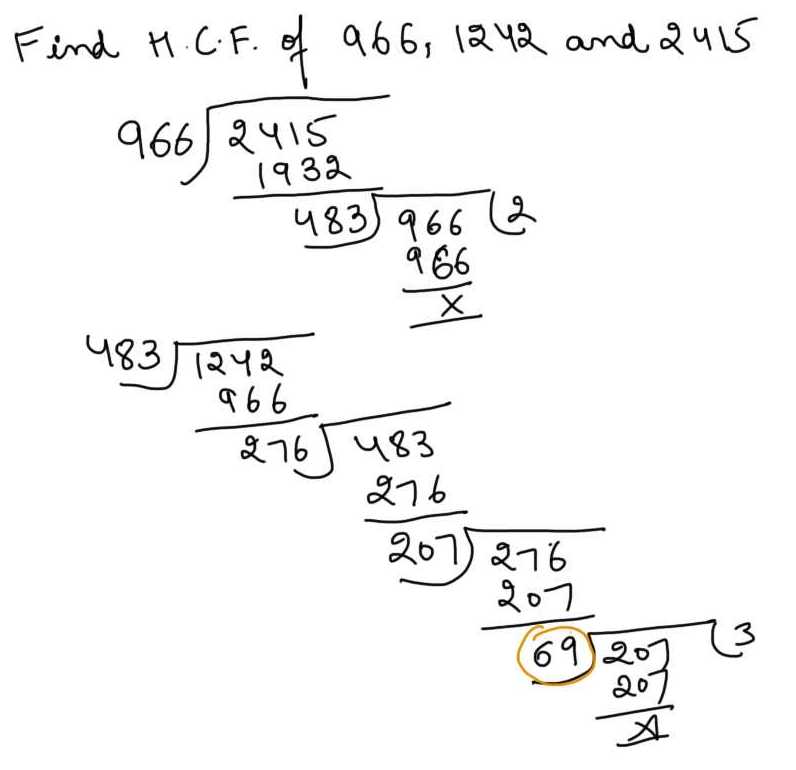H.C.F. of given numbers = 69	Let we have set of numbers. First of all, find the number  which divide at least two of the number in a given set of  number.remainder and not divisible numbers will carry forward as it is. Repeat the process until at least  two number is not divisible by any number except 1.The product of the divisor and the undivided numbers is the required L.C.M. Example: Find the L.C.M. of 12,36,48,72
H.C.F. & L.C.M. of Fractions	H.C.F. =  H.C.F. of Numerator / L.C.M. of Denominators	L.C.M. = L.C.M. of Numerator / H.C.F. of Denominators
Product of H.C.F. & L.C.M.	H.C.F * L.C.M. = product of two numbers
Decimal numbers	H.C.F. of Decimal numbers Step 1. Find the HCF of the given numbers without decimal. Step 2.Put the decimal point ( in the HCF of Step 1) from right to left according to the MAXIMUM  deciaml places among the given numbers.	L.C.M. of Decimal numbers Step 1. Find the LCM of the given numbers without decimal. Step 2.Put the decimal point ( in the LCM of Step 1) from right to left according to the MINIMUM  deciaml places among the given numbers.

Square & Cube 

• Square & Cube
• Square Root & Cube Root
• Factorization Method

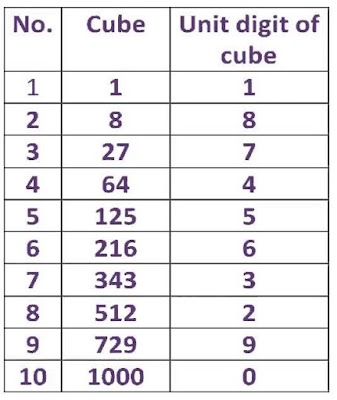
Perfect Square	Non-Perfect Square
last digit is 1, 4, 9, 6, 5	last digit is 2, 3, 7, 8

Square Root & Cube Root

• Fractions & Decimals

On Basis	Explanation
Decimal Fractions	A number with a denominator of power of 10 is a decimal fractions. 1/10= 1 tenth; 1/100= 0.1;38/100=0.38
Vulgar Fractions	Conversion of 0.64(decimal number) into a Vulgar Fraction.First of all write the numeric digit 1 in the denominator of a number (like here 0.64) and add as many numeric zeros as the digit in the number after decimal point.After that removes the decimal point from the given number.At last step just reduce the fraction to its lowest terms. So, 0.64 = 64/100=16/25;25.025 = 25025/1000 = 1001/4
Operations	Addition & Subtraction To perform the addition and subtraction of a decimal fraction could be done through placing them right under each other that the decimal points lie in one column. 3.424+3.28+.4036+6.2+.8+4   3. 424   3. 28     . 4036   6. 2     . 8 +4______ 18. 1076 Multiplication of a Decimal Fraction To find the multiplication of decimal fraction , first of all you need to remove the decimal point from the given numbers and then perform the multiplication after that assign the decimal point as many places after the number as the sum of the number of the decimal places in the given number. Step 1. 0.06*0.3*0.40 Step 2. 6*3*40=720 Step 3. 0.00720 Multiplication of a decimal fraction by power of 10 A multiplication of a decimal fraction by a power of 10 can be perform through shifting the decimal point towards right as many places as is the power of 10. like 45.6288*100=45628.8, 0.00452*100=0.452 Division
Comparison of Fractions	To compare the set of fractions numbers,first of all you need to convert each fraction number or value into a equal decimal value and then it will be became easy for you to assign them ( the numbers or value) in a particular way( ascending or descending order). 3/5,4/7,8/9 and 9/11 Arranging in Ascending Order 3/5= 0.6, 4/7 = 0.571, 8/9 = 0.88, 9/11 = 0.818. Now, 0.88 > 0.818 > 0.6 > 0.571 8/9>9/11>3/5>4/7
Recurring Decimal	Recurring Decimal A decimal number in which after a decimal point a number or set of number are repeated again and again are called recurring decimal numbers.It can be written in shorten form by placing a bar or line above the numbers which has repeated. 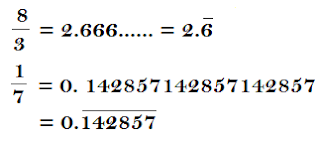Pure Recurring Decimal A decimal number in which all digits are repeated after a decimal point. Mixed Recurring Decimal A decimal number in which certain digits are repeated only.

• 
  

Surds & Indices 

• Some Rules of Indices
• Some Rules of Surds